Joining the dots: Mathematicians solve hot coloring problem

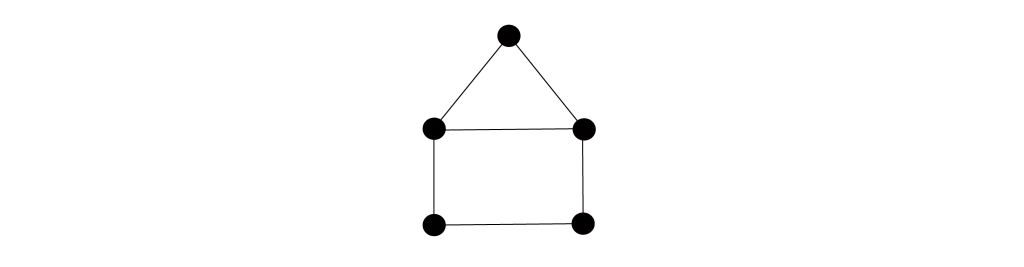
Have you ever tried to do the brainteaser below, where you have to connect the dots to make the outline of a house in one continuous stroke without going back over your lines? Or perhaps you’ve clicked on Facebook’s friend recommendations or played Settlers of Catan.

House challenge: Connect the dots to make the house in one continuous stroke without going back over your lines

If so, you’ve experienced a form of graph theory, a field of mathematics that fascinates Dr Xujun Liu from Xi’an Jiaotong-Liverpool University, China.

“My initial plan was to pursue a different field of mathematics, but I became captivated by the elegance and beauty of proof ideas in graph theory,” says Dr Liu.

From A to B

Graph theory is a branch of mathematics that explores the relationships and properties of graphs – but we’re not talking about pie charts and scatter plots.

Then what is a graph?

Say you wanted to work out the most efficient way to travel between London and Vienna by train. You could draw each city as a dot (called a vertex in mathematics), and the routes between the cities as lines or curves (called edges). This combination of vertices and edges makes up a graph.

The graph could then be used to study the connections and routes between the two cities.

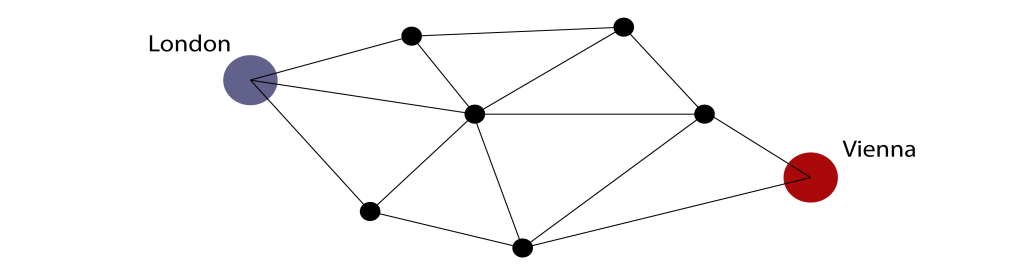
Travelling from London to Vienna by train: Possible routes through smaller cities are displayed as a graph

Graph theory can help mathematicians to model and analyse complex networks in various fields, including computer science and electrical engineering.

In collaboration with Dr Michael Santana and Dr Taylor Short from the Grand Valley State University, USA, Dr Liu has recently solved a problem that has attracted a lot of attention from graph theory researchers.

Colour me different

The team’s research involves an aspect of graph theory called coloring. The theory of coloring deals with the problem of labelling parts of a graph to comply with certain rules and avoid specific conflicts.

For example, imagine you wanted to colour each dot below so that there were never two dots of the same colour next to each other – this is an example of coloring.

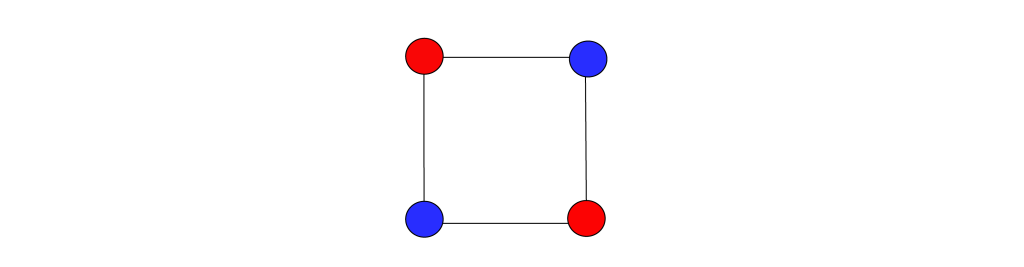
An example of coloring: A minimum of two colours is needed for the four dots if there are never two dots of the same colour next to each other

Dr Liu explains: “I work on a type of coloring called packing coloring, which is motivated by a frequency assignment problem in broadcast networks.

“There are many broadcast stations in the world, and we would like to assign each station a frequency; stations assigned the same frequency are required to be at least a certain distance apart, and each frequency requires a different smallest distance.

“One of the questions that arise from this problem is ‘what is the minimum number of frequencies needed for such an assignment?’”

Strategic development

In his most recent work, Dr Liu and his collaborators successfully solved a problem proposed by mathematicians Hocquard, Lajou, and Lužar in the Journal of Graph Theory in 2022.

This problem involves the division of subcubic graphs, where each vertex (dot) has a maximum of three edges (lines) attached to it.

The task is to determine how to partition the edges into multiple classes, considering that there are two distinct types of edges:

• Type I - requires that each pair of edges does not share an endpoint (each edge has two endpoints).

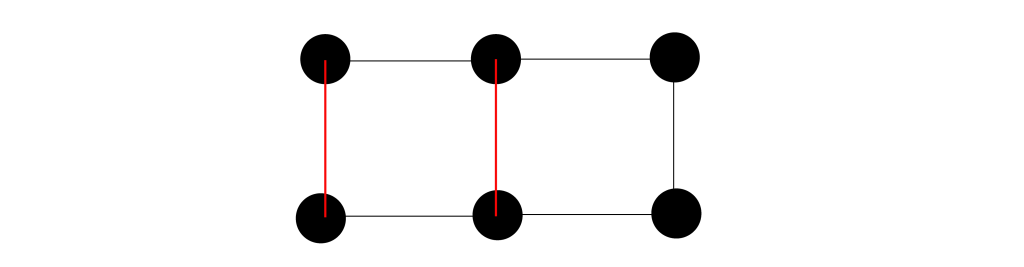
An example of a pair of edges that do not share an endpoint

• Type II -  requires that each pair of edges within it not only do not share an endpoint but also that their endpoints are not connected by another edge.

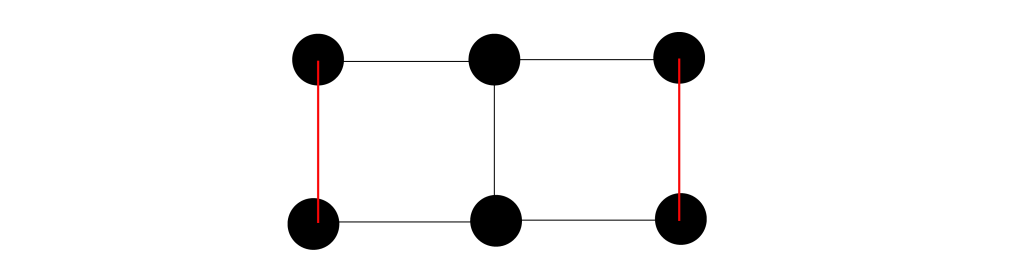
An example of two edges that do not share an endpoint and their endpoints are not connected by another edge

The question the team set out to solve is whether it is possible to minimise the number of type II classes  while keeping the number of type I classes fixed at one.

Dr Liu says: “By resolving this conjecture, we have made a significant contribution to enhancing our understanding of the structural properties of subcubic graphs and may provide insights to resolve the famous Erdős- Nešetřil conjecture.

“It may also provide guidance to solving problems in communication networks.”

Since Dr Liu made the decision to study graph theory under the PhD supervision of Professor Alexandr Kostochka at the University of Illinois, he has successfully solved several conjectures, including a problem proposed by the 2012 Abel Prize winner Szemerédi and his co-authors.

Dr Liu says he will continue to tackle more problems in the field. “I plan to continue researching graph coloring problems, focusing on exploring packing colorings via additional methodologies such as the Combinatorial Nullstellensatz and probabilistic methods.

“By pursuing these research directions, I hope to make meaningful contributions to the field,” he says.

The paper, “Every subcubic multigraph is (1,2^7)-packing edge-colorable”, is published in The Journal of Graph Theory.

Dr Liu has also received invitations to present this paper at numerous national and international conferences, including the 10th Conference on Combinatorics and Graph Theory in China and the 2023 Annual Conference of the Graph Theory and Combinatorics Association of the Operations Research Society of China.

Dr Xujun Liu talking at the 2023 Annual Conference of the Graph Theory and Combinatorics Association of the Operations Research Society of China

By Qinru Liu and Catherine Diamond

Edited by Patricia Pieterse